更新日:2022年11月18日
- 校長のつぶやき1
- 校長のつぶやき2
- 校長のつぶやき3
- 校長のつぶやき4
- 校長のつぶやき5
- 校長のつぶやき6
- 校長のつぶやき7
- 校長のつぶやき8
- 校長のつぶやき9
- 校長のつぶやき10
- 校長のつぶやき11
- 校長のつぶやき12
- 校長のつぶやき13
- 校長のつぶやき14
- 校長のつぶやき15
- 校長のつぶやき16
- 校長のつぶやき17
- 校長のつぶやき18
- 校長のつぶやき19
- 校長のつぶやき20-1(修学旅行編)
- 校長のつぶやき20-2(研修旅行編)
- 校長のつぶやき21
- 校長のつぶやき22
- 校長のつぶやき23
- 校長のつぶやき24
- 校長のつぶやき25
- R5校長のつぶやき1
- R5校長のつぶやき2
- R5校長のつぶやき3
- R5校長のつぶやき4
- R5校長のつぶやき5
- R5校長のつぶやき6
- R5校長のつぶやき7
- R5校長のつぶやき8
- R5校長のつぶやき9
- R5校長のつぶやき10
- R5校長のつぶやき11
- R5校長のつぶやき13
- R5校長のつぶやき14
- R5校長のつぶやき15-1(御殿場宿泊研修1日目編)
- R5校長のつぶやき15-2(御殿場宿泊研修2日目編)
- R5校長のつぶやき16
- R5校長のつぶやき17
- R5校長のつぶやき18
- R5校長のつぶやき19
- R5校長のつぶやき20
- R5校長のつぶやき21
- R5校長のつぶやき22
- R5校長のつぶやき23
- R5校長のつぶやき24
- R5校長のつぶやき25
- R6校長のつぶやき1
- R6校長のつぶやき2
- R6校長のつぶやき3
- R6校長のつぶやき4
- R6校長のつぶやき5
- R6校長のつぶやき6
- R6校長のつぶやき6-2
- R6校長のつぶやき7
- R6校長のつぶやき8
- R6校長のつぶやき9
- R6校長のつぶやき10
- R6校長のつぶやき11
- R6校長のつぶやき12
- R6校長のつぶやき13
- R6校長のつぶやき14
- R6校長のつぶやき15
- R6校長のつぶやき16
- R6校長のつぶやき17
- R6校長のつぶやき18
- R7校長のつぶやき1
- R7校長のつぶやき2
- R7校長のつぶやき3
- R7校長のつぶやき4
- R7校長のつぶやき5
- R7校長のつぶやき6
- R7校長のつぶやき10
- R7校長のつぶやき7
- R7校長のつぶやき8
- R7校長のつぶやき9
- R7校長のつぶやき11
- R7校長のつぶやき12
ここから本文です。
校長のつぶやき22
授業観察数学
校長 の内田です。
の内田です。
朝晩が、だいぶ寒くなってきました。つい先日まで暑くてエアコンをかけていたのに…季節は間違いなく、冬に向かっています。新型コロナもまた増えてきて、第8波の到来かとも言われています。みなさん、健康管理には十分気を付けてください。
さて、今日は授業観察のお話です。年に2回、授業観察があります。現在は後期の授業観察が始まっています。
テーマを決めて授業を行ってもらい、授業力の向上に努めてもらうために行っているもので、終わった後に授業に関して、指導・助言等を行います。日ごろから、午前部・午後部、各1回ずつは全教室を回っているので(最近は、忙しくて回れていません涙)、ほとんどの先生方の授業は見ているのですが、1時間中の最初から最後まで見ることができないのでとてもいい機会です。
今日は、2つの数学の授業を紹介したいと思います。(前期の授業です)一つはベテランの先生の授業で内容は「数学B等比数列」の授業です。もう一つは若手の先生の授業で「数学1平方根」の授業でした。
まずは、数学Bの等比数列の授業のお話から。
等差数列とか等比数列という言葉を久しぶりに聞きました。決められた規則に従って並んでいる列のことを数列といいます。
例えば
| (1)1,3,5,7,9,11…(2)1,2,4,8,16,32… |
(1)が等差数列で、(2)が等比数列です。
話の中で「初項」とか「公差」とか出てくるのですが、数列は高校時代にやっているので何となくはわかるのですが、言葉の意味をよく理解できていないというか、忘れてます。一般項の公式なんて全く記憶にないです。困った…。この等比数列の第〇項はいくつ?とか言われると??少ない数字なら計算していけばいいのでしょうけど、第〇項の〇が大きくなったときは一つ一つ計算をしていくわけにはいかないし…。
はぁ~。もう少しちゃんと数学を勉強しておけばよかった…。と言っても、高校時代はもう30数年前の話だし、高校時代は私立文系の選択をしていたので、3年生の時には数学もありませんでした。(数学が苦手だから文系なんですけど(汗))
先生が生徒に説明します。一緒になってお勉強。あっ、そういうことか!とてもわかりやすい説明です。板書も丁寧で、色分けして書かれているのでポイントがめちゃめちゃわかりやすかったです。聞いていて、「なるほど…」、「そういうことか」って思う場面が何回もありました。
できたとか、わかったと思わせてくれる授業は素敵ですね。わかる人に教えるのは簡単ですが、わからない人に教えるのは難しい。ちゃんと理解できていない私がわかるようになれば、わかりやすいってことでしょうか(笑)。私がわかりやすい授業のバロメーター?
隣にいた数学科の副校長に「数列が何のためにあるのか意味がわからん」と言ったら、丁寧に説明してくれました(笑)。
続いて数学1の平方根の授業。
まず最初に、本日の目標を板書します。「平方根を知ろう」。授業の始まりにその時間の目標や見通し(この時間に何をするのか)を明示することはとても大事ですね。ねらいは「平方根という概念を理解し、簡単な計算ができるようになる」ことだそうで…。目標がわかったような、わからないような…
問題に挑戦します。
下の方眼紙に面積1㎠、2㎠、4㎠、8㎠、の正方形を工夫して作ってみよう。(1マスが1㎠)
1㎠、4㎠は難しくはありません。
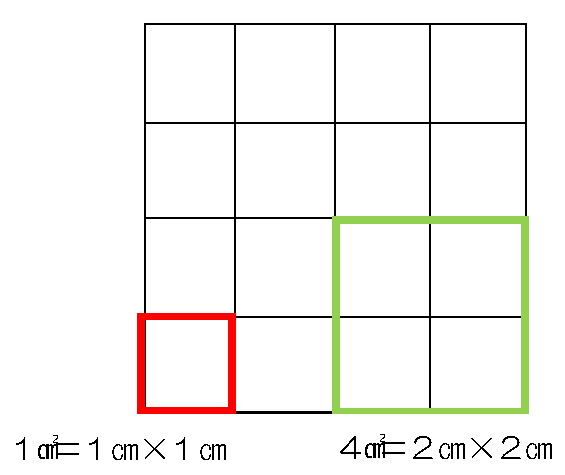 |
では2㎠は…
2㎠=√2cm×√2cm、√2は1.41421356…だから
|
1.41421356…(√2)→ |
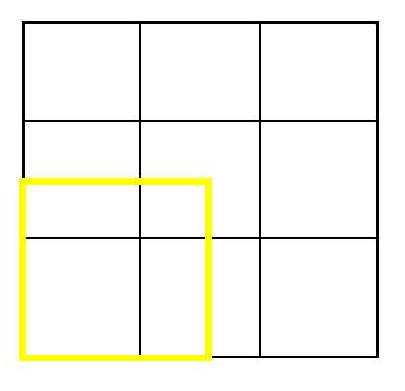 |
|
1.41421356…(√2)
|
う~ん、何か違和感がある…。1.41421356…の場所も正確ではないし。ちょっとできている子をカンニングさせてもらうと…。あ~~~っ衝撃!!
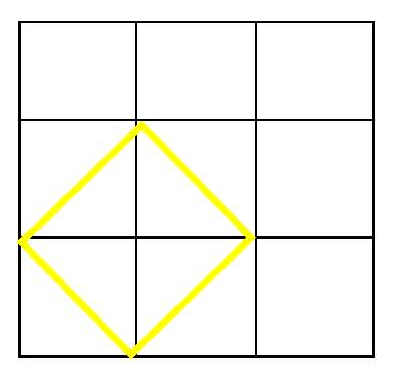
その子に「どうしてこうなったの?」と聞いてみました。「1マスが1㎠だから半分で0.5㎠、その半分が4つで2㎠」完璧な答え…。本当にすごいなぁ。その生徒の発想・ひらめきに感嘆!!私にはそう考えることができなかった。自分の発想力のなさ、頭の固さに落ち込む。はぁ~。自分の答えを副校長に見せると、「逆に知識が邪魔をするんですね」とのお答え。慰めにもならん…。確かにこの考え方をすれば8㎠を出すのも簡単。
この2つの授業、構造化されてとても分かりやすい授業、生徒の気づきを促す授業。どちらもいい授業でした。ありがとうございました。
おまけ
等差数列の授業が終わってからの副校長との会話
副校長が「フィボナッチ数列というのがあって、ひまわりの種の並び方はその数列どおりになっているんですよ」
はぁ?!フィボナッチ数列??聞いたこともない。その上、ひまわりの種の並び方が数列通り???はあぁ~???ばっかりだ。なんで自然界に数列が関係する???
納得がいかず、やっぱり調べてみる。
まずは、フィボナッチ数列
| 「1、1」から始まり、前の二つの数字を足したものをどんどん並べていったもの |
実際に書いてみるとこんな感じ
1,1,2,3,5,8,13,21,34,55,89…
1+1=2、1+2=3、2+3=5、3+5=8…って感じです。
そしてひまわりの話

渦巻き状に配置されている種
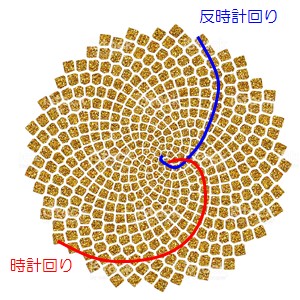
イラスト化するとこうなります。赤い線はらせん状の種の並びをしています。線はひまわりの中心から外側に向かって時計回りになっています。また、見方を変えると反時計回りに種が配置されているようにも見えます。
このように時計回りと反時計回りの種の配置を持つひまわりですが反時計回りの線の数は絶対に、
- 時計回りが21本、反時計回りが34本
- 時計回りが34本、反時計回りが55本
- 時計回りが55本、反時計回りが89本
なんでだぁ~~~~~~!!!
規則的な数字の並びがなぜ自然界に???
よけいにわからなくなった…。まつぼっくりやオウムガイもフィボナッチ数列が使われているとか。う~ん深い…。副校長曰く「世界は数理でできている」。
全く分からなくなったので今日はここまで(了)
